一、 案例背景
通過設計“嘉興南湖湖面有多大”、“某一時間段內高鐵行經的路程如何求”兩個紅色主題案例吸引學生的興趣,讓學生關注身旁的紅色元素和新時代的科技進步,激發學生的愛國情懷和民族自豪感。
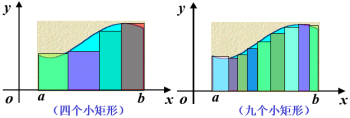
1.作為嘉興的在校大學生,肯定知道南湖,甚至不止一次去過南湖。嘉興南湖是中國共產黨的誕生地,是紅船精神的發源地。自然地,學生會問南湖有多大?南湖湖面并不是一個規則圖形,其邊界又不是直線,但通過分割,可以將其分解成若干矩形和曲邊梯形(梯形中的斜邊換成曲線)。所以,只要求出曲邊梯形的面積就可以計算出南湖的具體面積。

2.現在高鐵出行習以為常。我國的高鐵已處于世界領先水平,運營里程突破4萬公里,穩居世界第一。坐高鐵時經常會看到車廂里顯示的車速不規律地變來變去。想知道某時間段內經過的路程該怎么求呢?即,如何求一段時間內變速直線運動的路程。
二、主要做法
通過整體教學設計、本節課知識點、三維教學目標、問題引入、問題求解、問題提煉、形成概念,開展課堂教學,講解定積分的概念,感悟思政元素、感受科學精神。
1. 教學過程設計
(1)通過播放南湖的圖片和小視頻,讓學生看到南湖的全貌。問學生覺得南湖大不大,引導學生思考,激發學習興趣。
(2)通過分析,將南湖的面積歸結為求曲邊梯形的面積,培養學生的分析問題的能力。在求解曲邊梯形面積的過程中,培養學生“化整為零”、“以直代曲”、“積零成整”等數學思維,并介紹劉徽的“割圓法”,增強學生的文化自信。
(3)問學生是否有坐高鐵看到車內顯示速度的經歷,并播放相關視頻,提升課堂樂趣,并介紹我國高鐵發展情況,激發學生的民族自豪感。拋出路程問題,引發學生思考,并提示解決問題。
(4)提煉兩個案例的共同點,得出定積分的概念,培養學生數學歸納能力。
(5)總結本課所學的數學方法及課程思政感悟:分割近似再求和,所得結果欠精確。堅定理想取極限,積微成著把夢圓。
2. 知識點及教學目標
(1)知識點
定積分概念提出的背景、方法及其應用。
(2)三維教學目標
? 知識與技能:了解定積分概念提出的幾何背景和物理背景,體會“化整為零”、“以直代曲”(以常代變)、“無限逼近”的數學思想。
? 過程與方法:通過學生熟悉的案例,引出曲邊圖形的面積和變速直線運動的路程問題,讓學生了解定積分概念的來源和現實中的簡單應用。
? 情感態度與價值觀:通過南湖面積和高鐵路程問題的引入,學生能夠聯想到南湖是中國革命紅船起航地,高鐵是我們的國之重器,激發學生的愛國情懷和民族自豪感。
3. 問題引入
(1)如何求曲邊梯形的面積?
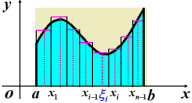
“化繁為簡,化未知為已知”是最主要的數學思想。如果將曲線變成直線就好了。直接“以直代曲”顯然誤差很大,即曲線越小替換成直線就越精確。因此,通過分割,把曲邊梯形分成許多小曲邊梯形,并用小矩形的面積近似代替小曲邊梯形的面積。當分割越細,所得的近似值越接近準確值,正如我國魏晉時期偉大的數學家劉徽說得那樣“割之彌細,所失彌少”。故,當每個小曲邊梯形的寬度趨于0時就得到其準確值。最后通過求小矩形面積之和的極限,得到曲邊梯形得面積。
(2)如何求變速直線運動的路程?
類似上例,將整個時間段分成若干小時間段,每段時間內近似看成勻速直線運動,將這些小時間段加起來,并讓每個時間間隔都趨于0,就得到所經過的路程。
4. 問題求解
(1)設曲邊梯形是由曲線
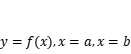 ,以及
,以及
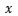 軸所圍成的,求其面積,這里不妨假設
軸所圍成的,求其面積,這里不妨假設
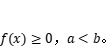
第一步:分割。把區間
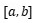 分成
分成
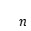 份;第
份;第
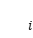 份的長度記為
份的長度記為
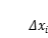 ,也就是把曲邊梯形分成了
,也就是把曲邊梯形分成了
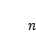 個很小的曲邊梯形。
個很小的曲邊梯形。
第二步:近似。把個小曲邊梯形近似看成一個小矩形,第
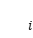 個小曲邊梯形的面積
個小曲邊梯形的面積
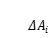 就近似的表示成一個小矩形的面積,不失一般性,小矩形的長取
就近似的表示成一個小矩形的面積,不失一般性,小矩形的長取
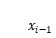 和
和
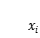 之間的任意一點
之間的任意一點
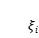 對應的函數值
對應的函數值
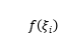 來表示,于是
來表示,于是
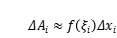 。
。
第三步:求和。整個曲邊梯形的面積就是這
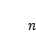 個小曲邊梯形的面積之和,故
個小曲邊梯形的面積之和,故
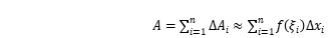 。
。
第四步:取極限。 要取到精確值,必須讓每一小塊非常接近矩形,也就是每個
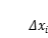 都要趨于
都要趨于
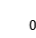 。為此,只需這
。為此,只需這
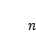 個
個
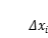 中最大趨于
中最大趨于
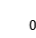 ,記
,記
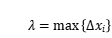 ,于是就得到了原曲邊梯形的面積精確值,即
,于是就得到了原曲邊梯形的面積精確值,即
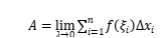 。
。
(2)設
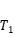 到
到
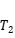 時刻內的速度為
時刻內的速度為
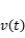 ,求這段時間經過的路程
,求這段時間經過的路程
 。
。
第一步:分割。把區間
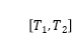 分成
分成
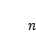 份;第
份;第
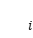 份的時長為
份的時長為
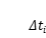 。
。
第二步:近似。把個小時段近似看成勻速直線運動,第
 個時段經過的路程
個時段經過的路程
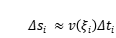 ,其中
,其中
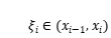 。
。
第三步:求和。 整段時間內經過的路程近似為
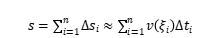 。
。
第四步:取極限。記
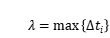 ,故
,故
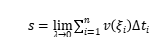 。
。
5. 問題提煉
上述兩例,分別是幾何問題和物理問題。雖然它們各屬不同學科,但解決問題的思想和方法是一樣的,把整體問題通過“化整為零”、“以直代曲”(或“以常代變”),再“積零為整”。即分割,近似,求和,取極限。拋開這些問題的具體背景,將此類問題的共性提煉出來,定義了求一種特定和式極限的重要數學工具──定積分。
定義:設函數
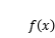 在區間
在區間
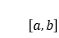 上連續,在
上連續,在
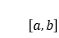 內任意插入
內任意插入
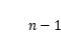 個分點
個分點
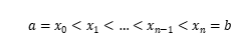 ,把區間分成
,把區間分成
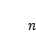 個小區間
個小區間
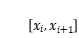 ,且每個小區間的長為
,且每個小區間的長為
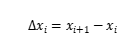 ,其中
,其中
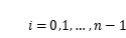 。在每個小區間
。在每個小區間
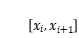 上任取一點
上任取一點
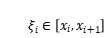 ,作和式
,作和式
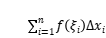 ,若不論對
,若不論對
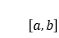 怎樣分法,也不論
怎樣分法,也不論
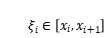 如何取法,只要當
如何取法,只要當
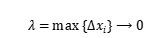 時,上述和式的極限總趨于一個確定的值
時,上述和式的極限總趨于一個確定的值
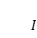 ,即
,即
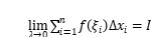 ,則稱
,則稱
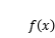 在區間
在區間
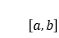 上可積,并將這個極限值
上可積,并將這個極限值
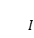 稱為函數
稱為函數
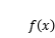 在區間
在區間
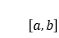 上的定積分,記作
上的定積分,記作
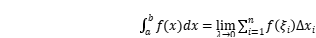 。
。
三、主要成效
通過對曲邊梯形面積和變速直線運動路程問題的介紹,理解了定積分的概念,體會了數學思維方法在解決現實問題的應用,了解了中國古代數學的杰出貢獻,領悟了數學發展過程中蘊含的處世哲理,激發了勇于擔當的時代責任感。
四、反思探討
今天所介紹的兩個案例,通過化整為零,先得到近似值,然后逐步逼近,最終求得精確值。生活中,我們要學會“化整為零”,將遇到的大困難分解成一些小困難,個個擊破。雖然不能直接到達目的地,但積微成著,逐步接近夢想,才能最終達到理想的彼岸。
經過眾多科學家的不懈努力,中國高鐵等高科技已經世界領先。作為新時代的大學生,要努力增強自身建設中國式現代化強國的科學素養和專業本領,勇擔時代重托和復興重任。
五、相關思政元素
堅定理想、百折不撓、文化自信、民族自豪感、真知、強能

